カウント値の割り当て
カードカウンティングのシステムをより有効にするためには、それぞれのカードの正確な価値を知る必要がある。
これを決定するために、基本戦略を使ってベンチマークを前提としたシングルデッキゲームのシミュレーションを行う。
既に言及したように、その期待値は-0.02%である。
次に、シングルデッキから2のカードを1枚だけ抜き、それ以外は同じ条件で再びシミュレーションをしてみる。
その結果は、期待値が+ 0.38%まで上がった。
この2つの期待値を比較した結果が、2のカードの価値を測定するものさしとなる。
今回のケースにおいて言えば、2のカードを取り除くことはプレイヤーにとって0.40%の価値があると分かる。
その他のカードのランクについても同様のプロセスを繰り返し行った。
その結果として、それぞれのカードの相対的価値を示した表を作成した(全ての数値はベンチマークのシングルデッキゲームにおける期待値の差異を表している)。
以下に示す表は、特定のランクのカードを排除することによって生じる期待値の差異をまとめたものだ。
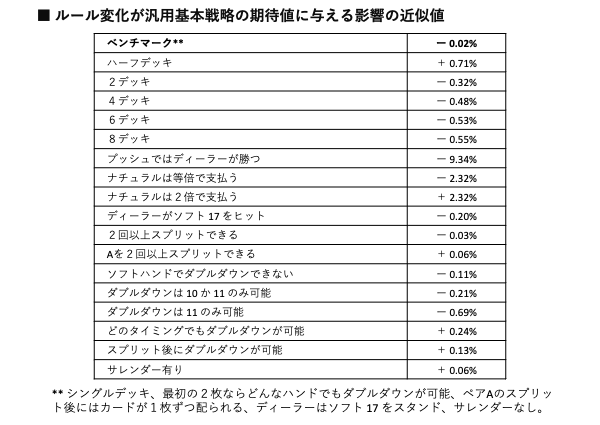
※基本戦略の使用を前提とする
例えば、シングルデッキから5のカードを1枚だけ取り除いた場合、プレイヤーの期待値の差異は+0.67%となる。
これでベンチマークのシングルデッキ(元々の期待値=-0.02%)では、その期待値が+ 0.65%に向上したことになる。
逆にAを1枚取り除くと、その期待値は-0.59%変化するのだ。
では、もしAと5が1枚ずつ取り除かれたらどうなるのか? 近似した値を出すには、単純に2つの差異を足せばいい。
よって差異の合計値は-0.59%(Aの差異) + 0.67%(5の差異)で + 0.08%となる。
このことから、Aと5の両方のカードを取り除くと、プレイヤーはほぼ振り出しに戻るといっていい。
この2枚はお互いを相殺し合ったのだ。
Aと5のカードの枚数を増減させたときの影響を見るために、図3を用意した(Aと5を例に挙げたのは、これらが、それぞれプラスとマイナスで最も大きな期待値の差異を生むからである)。
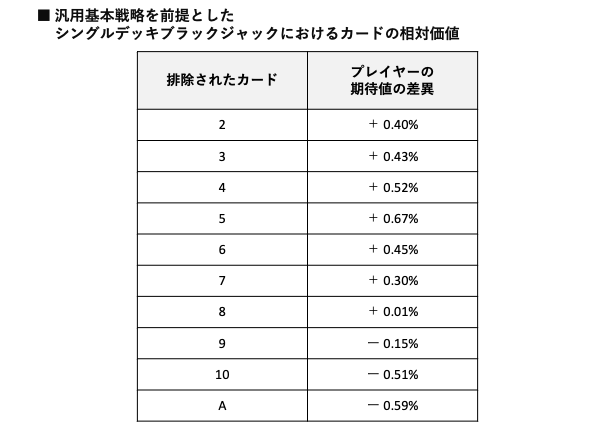
すでに述べたが、ハイカード(主にAと10)が少ないとき、プレイヤーは不利な状態である。
これは図3で確認できる。
シングルデッキからハイカードの数を減らしていくと期待値は下がっていく。
プレイヤーにとっては、デッキ中のハイカードが平均より多いことが好ましいのである。
ここから10のカードとAを「有利なカード」と呼ぶことにする。
図3 : 有利・不利の極端にあるAと5の増減による効果
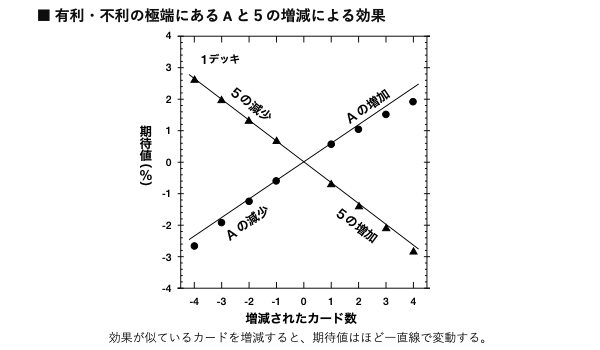
効果が似ているカードを増減すると、期待値はほぼ一直線で変動する。
同様に、ローカード(2~7)を減少させていくとプレイヤーの期待値は上昇する。
つまりローカードを減らすことで相対的にハイカードが多い状態になり、プレイヤーにとって有利となるのだ。
よって、ローカードは残りデッキに少ない状態が好ましいのである。
ここで、2~7を「不利なカード」と位置づけることにする。
では最後に、カードカウンティングの核心をまとめてみよう。
どのカードが残っているかを知るため、プレイヤーはプレイ済みカードをカウントしていく。
残りデッキの構成が変化するにつれて、有利なカードと不利なカードの割合の変化はプレイヤーを有利にしたり、不利にしたりする。
つまり重要なのは、プレイヤーがいつ有利で、いつ不利なのかを見極めることだ。
そして、有利なときには大きく、不利なときには小さくベットするのである。
こうすることで大きなベットによる勝ち分が、小さなベットの負け分を相殺する以上に大きな収益となるのだ。
その結果、長期的には有利に勝負できるのである。
関連ページ
- はじめに
- カジノのブラックジャックができる人気アプリやゲームのランキングサイトです。無料・有料問わず実際にプレイしてみてつけたランキングです。
- ガムボールをカウントする(キーカウント)
- カジノのブラックジャックができる人気アプリやゲームのランキングサイトです。無料・有料問わず実際にプレイしてみてつけたランキングです。
- ピポットとIRC
- カジノのブラックジャックができる人気アプリやゲームのランキングサイトです。無料・有料問わず実際にプレイしてみてつけたランキングです。
- 天はカードの上にカードを造る
- カジノのブラックジャックができる人気アプリやゲームのランキングサイトです。無料・有料問わず実際にプレイしてみてつけたランキングです。
- カードカウンティング――従来のスタイル
- カジノのブラックジャックができる人気アプリやゲームのランキングサイトです。無料・有料問わず実際にプレイしてみてつけたランキングです。
- まとめ
- カジノのブラックジャックができる人気アプリやゲームのランキングサイトです。無料・有料問わず実際にプレイしてみてつけたランキングです。